Extension of the flexible, polarizable, Thole-type model potential (TTM3-F, v. 3.0) to describe the vibrational spectra of water clusters and liquid water
The motivation of this work stems from the desire to establish the key elements that a classical model should take into account for a more realistic description of the vibrational spectra of water in different environments. Analysis of the IR bulk water spectra can provide detailed information concerning the liquid water structure and dynamics. To this end, an extension of the flexible, polarizable Thole-type model for water [J. Chem. Phys. 116, 5115 (2002); J. Phys. Chem. A 110, 4100 (2006)] is presented, based on modeling the different behavior of the water monomer in a condensed environment with respect to the gas phase.
Water monomer in different environments
In the gas phase, the lowest dissociation asymptote of a water molecule corresponds to the homolytic dissociation, viz.
whereas, in the condensed phase, the lowest dissociation asymptote correlates with the heterolytic products
This is because incremental solvation of the products eventually favors those charged with respect to the radical species, because the energetic stabilization of the former is much greater than the one of the latter.
The condensed phase behavior is modeled by an "effective," non-linear Dipole Moment Surface (DMS) that is a function of the intramolecular degrees of freedom
(
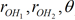) according to
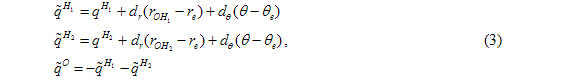
where
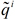are the "effective" charges
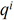are the charges derived from the Partridge-Schwenke (PS) DMS
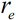and
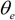are the equilibrium monomer bond length and bend angle
,
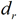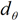are parameters.
The variation of the "effective" charge
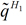with
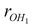and
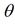is indicated in Figure 1, panels (a)-(b), for the gas phase, linear (constant charges) and "effective" DMSs, respectively. The "effective" DMS has the correct behavior of increasing charge on the hydrogen atom upon elongation of
.
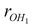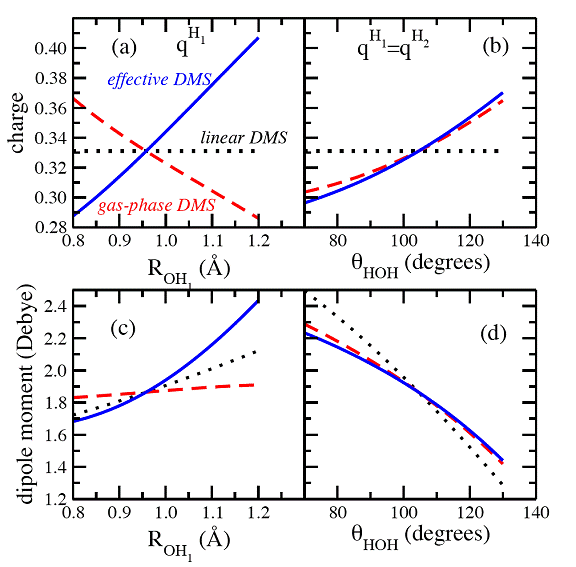
Figure 1. Atomic charges and total dipole moment for selected geometries of the water monomer. The dotted lines correspond to the linear Dipole Moment Surface (DMS) (constant charges), the dashed lines to the non-linear DMS (geometry dependent charges), and the solid lines to the non-linear "effective" DMS (see text for details). (a) The charge on the hydrogen (H1) atom as a function of the ROH1 distance (for ROH2 = Re and θ=θe), (b) The charge on the hydrogen (H1) and (H2) atoms as a function of the intramolecular bend-angle, θ (for ROH1 = ROH2 = Re), (c) and (d) the corresponding magnitude of the dipole moment for the geometries used in panels (a) and (b), respectively.
Functional form
As in the previous versions of the flexible model, an additional site (M-site) carries the charge instead of the oxygen atom. The position of the M-site is determined according to the holonomic constraint of Reimers et al.
where
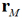and
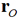are the position vectors of the M-site and the oxygen atom while
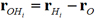. In the subsequent discussion, superscripts indicate the charges on the atomic sites (H1, H2, O) provided by the PS-DMS, whereas subscripts denote the partial charges on the charge sites (H1, H2, M-site) that are used in the model. The following transformation of the "effective" charges
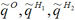leads to a new sets of charges
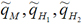with the same dipole moment,
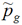, while a proper choice of the parameter
γ
yields a more accurate value for the quadrupole moment:
Therefore the PS-DMS atomic charges qi (i=H1, H2, O) are transformed to "effective atomic" charges
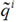(i=H1, H2, O) and then to "effective charge-site" charges
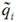(i=H1, H2, M-site) according to the scheme:
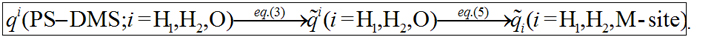
As in the previous versions of the potential, Thole's method was employed for the treatment of the electrostatic interactions. According to this scheme, an effective density replaces the interactions between point charges/dipoles. The density ρ(r) is expressed as:
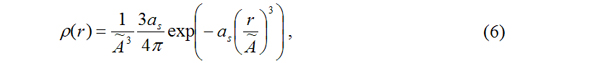
where the dimensionless parameter as determines the width of the density and à = (aiaj)1/6 with ai and aj being the atomic polarizabilities. In the present version, the oxygen atom carries neither a charge nor is associated with a polarizable site. Therefore the parameter à is determined only for interactions between the hydrogen atoms and the M-sites from the parameters aH and aM, which were chosen to be the same with the hydrogen and oxygen atomic polarizabilities, respectively (cf. Table I). In contrast to the previous versions of the model that employed three polarizable sites, the current version employs only one polarizable site located on the M-site. Note, the value of the M-site polarizability, a=1.444 Å3, used for the computation of the induction effects is different from the value aM=0.837 Å3 that determines the parameter à in equation (6).
The pairwise additive van der Waals (vdW) interaction between the oxygen atoms is described by the Buckingham exponential-6 potential:
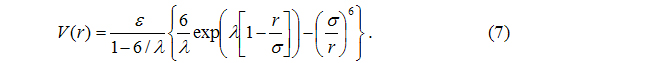
Table I. Parameters of the TTM3-F interaction potential for water.
Parameters |
TTM3-F |
|---|---|
σ(Å) |
3.632 |
ε(kcal/mol) |
0.175 |
λ |
13.5 |
as |
0.175 |
dr(e/Å) |
0.5 |
dθ (e/rad) |
0.012 |
aM (Å3) |
0.837 |
aH (Å3) |
0.496 |
γ |
0.46 |
a(Å3) |
1.444 |
Results
The O-O, O-H and H-H Radial Distribution Functions (RDFs) of liquid water from classical and quantum (P=32 beads) simulations together with the experimental results (including the experimental error bars) are shown in Figure 2(a). The comparison between the intramolecular O-H and H-H RDFs with versions 2.1 and 3 of the potential (both obtained with P=32) and the experimental data is shown in Figure 2(b).
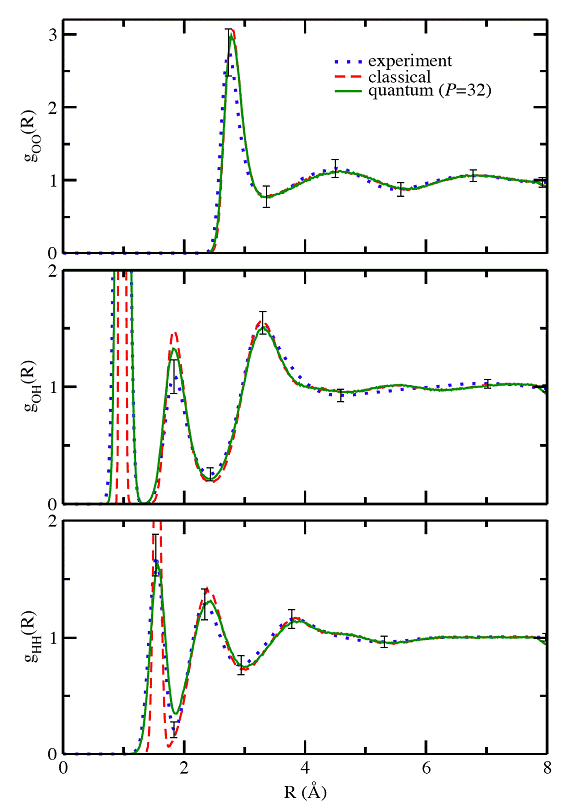
Figure 2(a). Liquid water oxygen-oxygen, oxygen-hydrogen and hydrogen-hydrogen Radial Distribution Functions at T=298.15 K. The solid line corresponds to experiment, the dashed lines to the quantum (P=32 beads), and the dotted-dashed lines to the classical statistical mechanical results. The experimental error bars are also indicated.
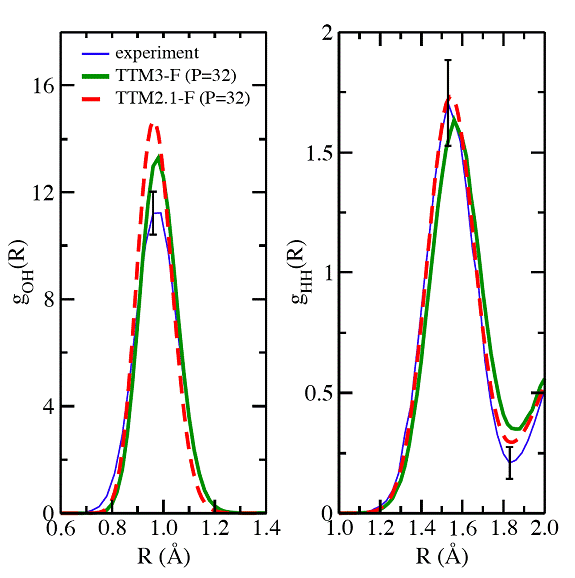
Figure 2(b). The intramolecular oxygen-hydrogen and hydrogen-hydrogen radial distribution functions from quantum statistical mechanical (P=32 beads) simulations.
The IR spectra of liquid water computed with the TTM3-F potential during a classical simulation at ρ=0.997 gr/cm3 with the inclusion of harmonic quantum corrections is compared to the experimental results in Figure 3. The shape of the spectra is similar especially in the 3,000-4,000 cm-1 region that corresponds to the OH stretching vibrations.
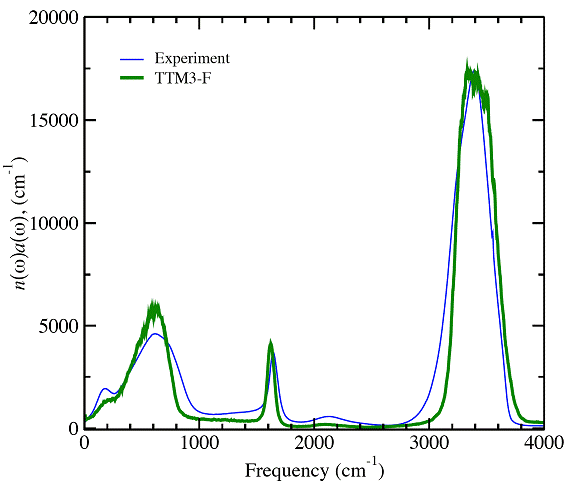
Figure 3. The IR spectra of liquid water obtained from classical simulations with the TTM3-F potential. The experimental results are also indicated.
The gas-to-liquid energy difference obtained from the classical MD and the quantum (CMD) simulations as a function of the number of beads, P, for both the U0 and UT estimators is listed in Table II. The results suggest that ΔE converges to -10.8±0.1 kcal/mol with the 2 estimators used in this study for P=32. The corresponding heat of vaporization ΔHv(= –ΔE + kβT) with the TTM3-F potential is 11.4±0.1 kcal/mol.
The new version (3.0) predicts a value of -271 atm (P=32) for the pressure at the experimental density (ρ =0.997 gr/cm3), a significant improvement over the value of -1800 ± 385 atm obtained with the previous version 2.1.
The classical and quantum (NPT) simulations predict that the liquid density at T=298.15 K and P=1 atm is 0.994 gr/cm3 and 1.008 gr/cm3 (for 32 beads), respectively.
The magnitude of quantum effects (difference between the P=1 and P=32 results) with the TTM3-F potential amounts to just 0.1 kcal/mol, a finding that is significantly different than the corresponding (P=32) result of 1.01±0.02 kcal/mol obtained with the previous version (TTM2.1-F) of the potential. The two versions have similar values for the heat of vaporization (TTM3-F: 11.4±0.1 kcal/mol, TTM2.1-F: 11.25±0.02 kcal/mol), despite the fact that the magnitude of the quantum effects between the two versions differs by almost 1 kcal/mol. The difference between the two versions mainly lies in the description of the intramolecular potential and dipole moment surfaces.
Table II. Results of the classical and quantum molecular dynamical simulations in the (NVT) ensemble with a cell of N=128 water molecules. (a) (NPT) ensemble and N=128 molecules. (b) (NVT) ensemble and N=256 molecules. The energy is expressed in kcal/mol, the pressure P in atm. P denotes the number of beads used in the quantum statistical mechanical simulations.
P |
N |
 |
 |
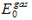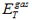ΔE0 |
ΔET |
Pressure, P |
<rOH> |
<θHOH> |
1 |
128 |
3.55 |
-10.712 |
54 |
0.9861 |
105.45 |
||
2 |
128 |
5.175 |
32.501 |
-10.012 |
-14.496 |
-16 |
0.9880 |
105.35 |
4 |
128 |
7.815 |
20.383 |
-9.768 |
-12.118 |
-116 |
0.9926 |
105.35 |
8 |
128 |
11.048 |
16.142 |
-10.012 |
-11.145 |
-138 |
0.9990 |
105.29 |
16 |
128 |
13.475 |
15.170 |
-10.419 |
-10.844 |
-152 |
1.0035 |
105.20 |
32 |
128 |
14.571 |
15.048 |
-10.671 |
-10.795 |
-271 |
1.0052 |
105.13 |
32(a) |
128 |
14.571 |
15.048 |
-10.690 |
-10.815 |
1.0 |
1.0052 |
105.15 |
1 |
256 |
3.55 |
-10.713 |
64 |
||||
2 |
256 |
5.175 |
32.501 |
-9.980 |
-14.480 |
16 |
||
4 |
256 |
7.815 |
20.383 |
-9.783 |
-12.141 |
-59 |
In conclusion, we have demonstrated that the inclusion of a phenomenological monomer DMS is able to capture the main features of the vibrational spectra of water both in the gas and the liquid phases. The new model produces results of comparable accuracy for the structural and energetic properties of water clusters and liquid water and a significantly better value for the pressure at T=298 K, when compared to the previous versions. It furthermore yields accurate vibrational spectra for the OH stretching vibrations in both clusters and liquid water. To the best of our knowledge, this is the first time that this result is achieved by a classical molecular interaction potential.
For more information about the new model see, G. S. Fanourgakis and S. S. Xantheas, Journal of Chemical Physics 128, 074506 (2008)
Acknowledgments: This work was supported by the Division of Chemical Sciences, Geosciences and Biosciences, Office of Basic Energy Sciences, US Department of Energy. Battelle operates the Pacific Northwest National Laboratory for the US Department of Energy.
Notice: This computer software was prepared by Battelle Memorial Institute, hereinafter the Contractor, under Contract No. DE-AC05-76RL0 1830 with the Department of Energy (DOE). All rights in the computer software are reserved by DOE on behalf of the United States Government and the Contractor as provided in the Contract. NEITHER THE GOVERNMENT NOR THE CONTRACTOR MAKES ANY WARRANTY, EXPRESS OR IMPLIED, OR ASSUMES ANY LIABILITY FOR THE USE OF THIS SOFTWARE. This notice including this sentence must appear on any copies of this computer software. Download (tar.gz file 20kb) a Fortran-90 subroutine with the new version of the TTM3-F potential (energies and gradients).